Medias de posición

Dividen un conjunto de datos en grupos con el mismo número de individuos. Valores de la variable estadística que dejan por debajo de sí determinada cantidad de los datos. Son, en definitiva, una generalización del concepto de la mediana. Mientras que ésta deja por debajo de sí al 50% de la distribución, los cuantiles pueden hacerlo con cualquier otro porcentaje. Se denominan medidas de posición porque informan, precisamente, de la posición que ocupa un valor dentro de la distribución de datos.

Cuartiles: Son los tres valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales. Q1, Q2 y Q3 determinan los valores correspondientes al 25%, al 50% y al 75% de los datos. Q2 coincide con la mediana.

Calculo de los cuartiles

1. Ordenamos los datos de menor a mayor
2. Buscamos el lugar que ocupa cada cuartil mediante la expresion

Número impar de datos

2, 5, 3, 6, 7, 4, 9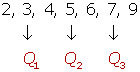

Número par de datos 

2, 5, 3, 4, 6, 7, 1, 9

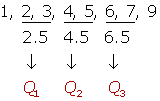
Calculo de los cuartiles para datos agrupados

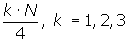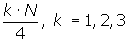En primer lugar buscamos la clase donde se encuentra  , en la tabla de las frecuencias acumuladas.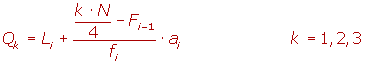

• Li es el límite inferior de la clase donde se encuentra la mediana.
• N es la suma de las frecuencias absolutas.
• Fi-1 es la frecuencia acumulada anterior a la clase mediana.
• ai es la amplitud de la clase.

Deciles: son los nueve valores que dividen la serie de datos en diez partes iguales. Los deciles dan los valores correspondientes al 10%, al 20%... y al 90% de los datos. D5 coincide con la mediana.

Calculo de los deciles

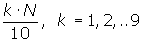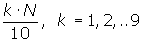En primer lugar buscamos la clase donde se encuentra  , en la tabla de las frecuencias acumuladas.

• Li es el límite inferior de la clase donde se encuentra la mediana.
• N es la suma de las frecuencias absolutas.
• Fi-1 es la frecuencia acumulada anterior a la clase mediana.
• ai es la amplitud de la clase.

  Percentiles: son los 99 valores que dividen la serie de datos en 100 partes iguales. Dan los valores correspondientes al 1%, al 2%... y al 99% de los datos. P50 coincide con la mediana.

Calculo de los percentiles

En primer lugar buscamos la clase donde se encuentra , en la tabla de las frecuencias acumuladas.

• Li es el límite inferior de la clase donde se encuentra la mediana.
• N es la suma de las frecuencias absolutas.
• Fi-1 es la frecuencia acumulada anterior a la clase mediana.
• ai es la amplitud de la clase.

Medidas de centralizacion

Habitualmente necesitamos disponer de un valor numérico que represente la disparidad de datos de una distribución de frecuencias. Estos valores son los llamados parámetros centrales o medidas de centralización, ya que son valores "intermedios" que se sitúan alrededor del centro de la distribución.

Media aritmética: es la cantidad total de la variable distribuida a partes iguales entre cada observación. 
Una de las limitaciones de la media aritmética es que se trata de una medida muy sensible a los valores extremos; valores muy grandes tienden a aumentarla mientras que valores muy pequeños tienden a reducirla, lo que implica que puede dejar de ser representativa de la población.

La media aritmética se calcula sumando todos los componentes y dividiendo el resultado entre el número de componentes. El resultado entero o decimal es la media aritmética.
Dados los n númerosla media aritmética se define como:

Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:

Se utiliza la letra X con una barra horizontal sobre el símbolo para representar la media de una muestra  , mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.

Mediana: es la puntuación de la escala que separa la mitad superior de la distribución y la inferior, es decir divide la serie de datos en dos partes iguales.

Existen dos métodos para el cálculo de la mediana:

1- Considerando los datos en forma individual, sin agruparlos.

Sean  los datos de una muestra ordenada en orden creciente y designando la mediana como .

a) Si n es impar, la mediana es el valor que ocupa la posición   una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir:  

b) Si n es par, la mediana es la media aritmética de los dos valores centrales. Los dos datos que están en el centro de la muestra ocupan las posiciones   y  .  Es decir: 

2- Utilizando los datos agrupados en intervalos de clase.

Al tratar con datos agrupados, si    coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:

 Moda: es el valor con una mayor frecuencia en una distribución de datos. Si todas las variables tienen la misma frecuencia diremos que no hay moda. El intervalo modal es el de mayor frecuencia absoluta. Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal.

La moda, cuando los datos están agrupados, es un punto que divide al intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:

Siendo la frecuencia absoluta del intervalo modal las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al intervalo modal.

Para obtener la moda en datos agrupados se usa la siguiente fórmula:

Donde:

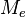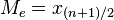
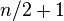
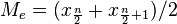
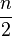
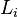 =  inferior de la clase modal.

 = es el delta de frecuencia absoluta modal y la frecuencia absoluta premodal.

 = es el delta de frecuencia absoluta modal y la frecuencia absoluta postmodal.

 = Amplitud del intervalo modal.

Parámetros estadísticos

Un parámetro estadístico es un número que se obtiene a partir de los datos de una distribución estadística. 

• Sirven para sintetizar la información dada por una tabla o por una gráfica.
• Son una consecuencia inevitable del propósito esencial de la estadística: crear un modelo de la realidad.

El estudio de una gran cantidad de datos individuales de una población puede ser farragoso e inoperativo, por lo que se hace necesario realizar un resumen que permita tener una idea global de la población, compararla con otras, comprobar su ajuste a un modelo ideal, realizar estimaciones sobre datos desconocidos de la misma y, en definitiva, tomar decisiones. A estas tareas contribuyen de modo esencial los parámetros estadísticos.

Tipos de frecuencias

Frecuencia absoluta: de un valor de la variable estadística X es el número de veces que aparece ese valor en el estudio. Se suele denotar por Fi la frecuencia absoluta del valor X = xi de la variable X. Dada una muestra de N elementos, la suma de todas las frecuencias absolutas debe dar el total de la muestra estudiada N.

Frecuencia relativa: (fi), es el cociente entre la frecuencia absoluta y el tamaño de la muestra (N). Es decir,

siendo el fi para todo el conjunto i. Se presenta en una tabla o nube de puntos en una distribución de frecuencias.
Si multiplicamos la frecuencia relativa por 100 obtendremos el porcentaje o tanto por ciento (pi).

Frecuencia absoluta acumulada: (Ni), es el número de veces ni en la muestra N.

Frecuencia relativa acumulada: (Fi), es el cociente entre la frecuencia absoluta acumulada y el total de la muestra.

Distribución de frecuencias

En estadística, se le llama distribución de frecuencias a la agrupación de datos en categorías mutuamente excluyentes que indican el número de observaciones en cada categoría.

 Esto proporciona un valor añadido a la agrupación de datos. Presenta las observaciones clasificadas de modo que se pueda ver el número existente en cada clase.