Habitualmente necesitamos disponer de un valor numérico que represente la disparidad de datos de una distribución de frecuencias. Estos valores son los llamados parámetros centrales o medidas de centralización, ya que son valores "intermedios" que se sitúan alrededor del centro de la distribución.
 Media aritmética: es la cantidad total de la variable distribuida a partes iguales entre cada observación.
Una de las limitaciones de la media aritmética es que se trata de una medida muy sensible a los valores extremos; valores muy grandes tienden a aumentarla mientras que valores muy pequeños tienden a reducirla, lo que implica que puede dejar de ser representativa de la población.
Media aritmética: es la cantidad total de la variable distribuida a partes iguales entre cada observación.
Una de las limitaciones de la media aritmética es que se trata de una medida muy sensible a los valores extremos; valores muy grandes tienden a aumentarla mientras que valores muy pequeños tienden a reducirla, lo que implica que puede dejar de ser representativa de la población.
La media aritmética se calcula sumando todos los componentes y dividiendo el resultado entre el número de componentes. El resultado entero o decimal es la media aritmética.
Dados los n números la media aritmética se define como:
la media aritmética se define como:
Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:
Se utiliza la letra X con una barra horizontal sobre el símbolo para representar la media de una muestra  , mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
, mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
Mediana: es la puntuación de la escala que separa la mitad superior de la distribución y la inferior, es decir divide la serie de datos en dos partes iguales.
Existen dos métodos para el cálculo de la mediana:
1- Considerando los datos en forma individual, sin agruparlos.
Sean  los datos de una muestra ordenada en orden creciente y designando la mediana como
los datos de una muestra ordenada en orden creciente y designando la mediana como 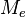
.
a) Si n es impar, la mediana es el valor que ocupa la posición  una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir:
una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir: 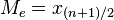
b) Si n es par, la mediana es la media aritmética de los dos valores centrales. Los dos datos que están en el centro de la muestra ocupan las posiciones  y
y 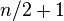 . Es decir:
. Es decir: 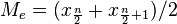
2- Utilizando los datos agrupados en intervalos de clase.
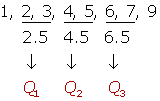
Al tratar con datos agrupados, si 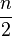 coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:
coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:
 Moda: es el valor con una mayor frecuencia en una distribución de datos. Si todas las variables tienen la misma frecuencia diremos que no hay moda. El intervalo modal es el de mayor frecuencia absoluta. Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal.
Moda: es el valor con una mayor frecuencia en una distribución de datos. Si todas las variables tienen la misma frecuencia diremos que no hay moda. El intervalo modal es el de mayor frecuencia absoluta. Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal.
La moda, cuando los datos están agrupados, es un punto que divide al intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:
Siendo la frecuencia absoluta del intervalo modal las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al intervalo modal.
Para obtener la moda en datos agrupados se usa la siguiente fórmula:
Donde:
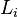
=

inferior de la clase modal.

= es el delta de frecuencia absoluta modal y la frecuencia absoluta premodal.

= es el delta de frecuencia absoluta modal y la frecuencia absoluta postmodal.

= Amplitud del intervalo modal.





























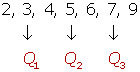
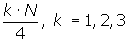
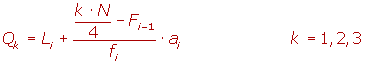
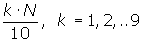










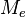 .
.
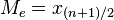

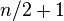
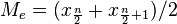
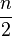



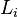 =
=  inferior de la clase modal.
inferior de la clase modal. = es el delta de frecuencia absoluta modal y la frecuencia absoluta premodal.
= es el delta de frecuencia absoluta modal y la frecuencia absoluta premodal. = es el delta de frecuencia absoluta modal y la frecuencia absoluta postmodal.
= es el delta de frecuencia absoluta modal y la frecuencia absoluta postmodal. = Amplitud del intervalo modal.
= Amplitud del intervalo modal.