Medidas de forma

Son medidas que determinan numéricamente algunas características de la forma en que estan distribuidos los datos. Entre estas medidas se tiene: el coeficiente de asimetría y el coeficiente de curtosis.


Coeficiente de asimetría: Se dice que una distribución de datos estadísticos es simétrica cuando la línea vertical que pasa por su media, divide a su representación gráfica en dos partes simétricas. Ello equivale a decir que los valores equidistantes de la media, presentan la misma frecuencia. En las distribuciones simétricas los parámetros media, mediana y moda coinciden, mientras que si una distribución presenta cierta asimetría, de un tipo o de otro, los parámetros se sitúan como muestra el siguiente gráfico:

Ello puede demostrarse fácilmente si se tiene en cuenta la atracción que la media aritmética siente por los valores extremos, que ya se ha comentado más arriba y las definiciones de mediana (justo en el centro de la distribución, tomando el eje de abscisas como referencia) y moda (valor que presenta una ordenada más alta).

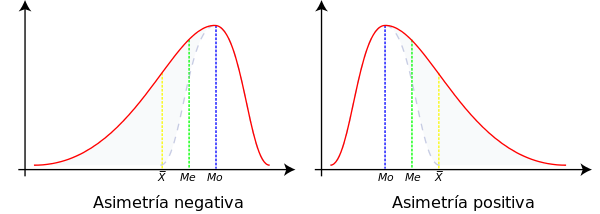
Por consiguiente, la posición relativa de los parámetros de centralización pueden servir como una primera medida de la simetría de una distribución.

Medidas de curtosis: Con estos parámetros se pretende medir cómo se reparten las frecuencias relativas de los datos entre el centro y los extremos, tomando como comparación la campana de Gauss. El parámetro usado con más frecuencia para esta medida es el coeficiente de curtosis de Fisher, definido como:

La comparación con la distribución normal permite hablar de distribuciones platicúrticas o más aplastadas que la normal; distribuciones mesocúrticas, con igual apuntamiento que la normal; y distribuciones leptocúrticas, esto es, más apuntadas que la normal.
Por último, existen otras medidas para decidir sobre la forma de una distribución con ajuste a modelos menos usuales como los que se muestran en las siguientes gráficas: