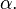Variables o atributos

Variables cuantitativas

• Discreta: son aquellas que sólo pueden tomar valores enteros como 1, 2, 3. En este sentido, los hermanos en una familia podrán ser: 1, 2, 3..., etc. Sin embargo, nunca podrán ser 1.5 o 2.3.
• Continua: son aquellas que pueden tomar cualquier valor real dentro de un intervalo o rango. Por ejemplo, los litros de leche ordeñados podrán se 1.5 o 10.3 etc. 

Variables cualitativas

• Nominales: son datos que corresponden a categorías que por su naturaleza no admiten un orden. Por ejemplo: sexo, carrera de estudio: economía, psicología, administración, etc.
• Ordinales: son aquellos que corresponden a evaluaciones subjetivas que se pueden ordenar o jerarquizar. Por ejemplo: en una competencia artística las posiciones de los ganadores se ordenan o jerarquizan en primer lugar, segundo lugar, tercer lugar, cuarto lugar, etc.

Estadística

Es una ciencia que nos permite tomar decisiones optimas en caso de incertidumbre. Es la herramienta fundamental que permite llevar a cabo el proceso relacionado de la estadística con la investigación científica. Es transversal a una amplia variedad de disciplinas, desde la física hasta las ciencias sociales, desde las ciencias de la salud hasta el control de calidad.

La estadística se divide en dos grandes áreas:

• Estadística descriptiva: parte que se encarga de describir los datos, esto es, de realizar un resumen y describir sus propiedades típicas. (Población)
• Inferencia estadística: parte que elabora conclusiones a partir de una muestra de los datos, en otras palabras, comprueba el ajuste de los datos a determinadas condiciones y proporciona una medida de la bondad de los mismos en términos probabilistas. (Muestra)

Gráficas de funciones trigonométricas haciendo uso del programa Graph

Este programa se puede descargar desde http://graph-1-2-1.softonic.com/

Funciones trigonométricas básicas

• Seno

En matemáticas el seno es una función continua y 2 π periódica es una función trascendente, su nombre se abrevia por sen

En trigonometria, el seno de un ángulo en un triángulo rectángulo de ángulo se define como la razón entre el cateto opuesto al ángulo y la hipotenusa:

O también como la ordenada correspondiente a un punto que pertenece a una circunferencia unitaria centrada en el origen (c=1):

Gráfica de Seno

• Coseno

Triángulo rectángulo en un sistema de coordenadas cartesianas.

En trigonometría, el coseno (abreviado cos) de un ángulo agudo en un triángulo rectángulo se define como la razón entre el cateto adyacente a dicho ángulo y la hipotenusa:

En virtud del Teorema de Tales, este número no depende del triángulo rectángulo escogido y, por lo tanto, está bien construido y define una función del ángulo  

Otro modo de obtener el coseno de un ángulo consiste en representar éste sobre la circunferencia unitaria centrada en el origen. En este caso el valor del coseno coincide con la abscisa del punto de intersección del ángulo con la circunferencia. Esta construcción es la que permite obtener el valor del coseno para ángulos no agudos.

Gráfica de Coseno

• Tangente

En trigonometría, la tangente (abreviado tan) de un ángulo (en un triángulo rectángulo) se define como la razón entre el cateto opuesto y el adyacente:

O también como la relación entre el seno y el coseno:

Representación en un círculo unitario el seno, coseno y la tangente de un ángulo.

Representación gráfica

¿Que son las funciones trigonométricas?

En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos. Son de gran importancia en:

• física
• astronomía, 
• cartografía,
• náutica, 
• telecomunicaciones
• la representación de fenómenos periódicos, etc.

Las funciones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.