Animatemática!!!: Funciones trigonométricas básicas

Seno

En matemáticas el seno es una función continua y 2 π periódica es una función trascendente, su nombre se abrevia por sen

En trigonometria, el seno de un ángulo

en un triángulo rectángulo de ángulo

se define como la razón entre el cateto opuesto al ángulo y la hipotenusa:

$\sen \alpha=\frac{a}{c}$

O también como la ordenada correspondiente a un punto que pertenece a una circunferencia unitaria centrada en el origen (c=1):

$\sen \alpha=a \,$

Gráfica de Seno

Coseno

Triángulo rectángulo en un sistema de coordenadas cartesianas.

En trigonometría, el coseno (abreviado cos) de un ángulo agudo en un triángulo rectángulo se define como la razón entre el cateto adyacente a dicho ángulo y la hipotenusa:

$\cos\alpha = \frac{b}{c}$

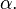
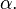
En virtud del Teorema de Tales, este número no depende del triángulo rectángulo escogido y, por lo tanto, está bien construido y define una función del ángulo $\alpha.$

Otro modo de obtener el coseno de un ángulo consiste en representar éste sobre la circunferencia unitaria centrada en el origen. En este caso el valor del coseno coincide con la abscisa del punto de intersección del ángulo con la circunferencia. Esta construcción es la que permite obtener el valor del coseno para ángulos no agudos.

Gráfica de Coseno

Tangente

En trigonometría, la tangente (abreviado tan) de un ángulo (en un triángulo rectángulo) se define como la razón entre el cateto opuesto y el adyacente:

$\tan(\alpha) = \frac{a}{b}$